A transport system with passengers traveling between stations in periodically arriving cabins is considered. We propose and evaluate an access control algorithm that dynamically limits the number of passengers who are allowed to board the current cabin. Simulation of a ski lift using empirical passenger data suggests that such access control can balance out the average waiting times at different stations. The algorithm works well with estimated values of the arrival and de-boarding rates.
By Pasquale Grippa, Evsen Yanmaz, Paul Ladinig, and Christian Bettstetter
Public transport systems have a broad range of design options and control mechanisms for improving the passenger throughput and travel experience. For example, they can be either schedule-based or on demand, fixed or adaptive to passenger load, and may or may not provide feedback to passengers and implement travel redirection. Regardless of the requirements and constraints, a passenger flow control can be an effective and economical method of reducing congestion and deadlock, while guaranteeing reliability and safety.
To contribute to this domain, we propose and evaluate an access control algorithm for implementation in the boarding areas of ski resorts, where customers use fixed-capacity, fixed-speed cabins between stations. Based on real-time knowledge of passenger arrival and queuing conditions at all the stations, the algorithm adaptively reports as to how many passengers are allowed to enter the next cabin. Metaphorically speaking, it acts as a guard for the cabins. The objective is to automatically improve passenger comfort and fairness by having waiting times in the same order of magnitude at all stations. The concept is evaluated by simulation using real passenger data obtained from the Austrian ski resort Bad Gastein, where it was tested by an industrial partner.
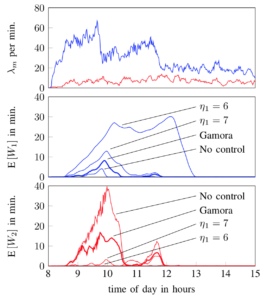
The algorithm, called Gamora (see comic figure in photo), computes the maximum number of passengers who can enter the next cabin. As input, it takes the average number of passengers in the cabins arriving at the first station, arrival rate at all stations, number of passengers waiting at all stations, probability of leaving at all stations, interarrival time between cabins, and cabin capacity. It computes the scaled stability thresholds, determines which stations need additional capacity, and returns the maximum number of passengers who can enter the next cabin, given the measured arrival rates, so that the scaled stability thresholds are equalized.
Gamora’s performance is compared to that of no control and static control. The latter reserves a fixed number of seats at the ground station for use at succeeding stations. Our simulation results show that Gamora achieves the best balance of waiting times at the stations (see figure).
In real scenarios, the parameters of the stochastic processes regulating passengers’ arrival and leaving are not known and have to be estimated. According to our results, Gamora is robust with respect to the estimation of these parameters.
Publication
Pasquale Grippa, Evşen Yanmaz, Paul Ladinig, and Christian Bettstetter. Guarded by Gamora: How Access Control Balances Out Waiting Times in Transport Systems. In Proc. IEEE Intern. Conf. on Intelligent Transportation Systems (ITSC), Maui, Hawaii, USA, November 4–7, 2018.