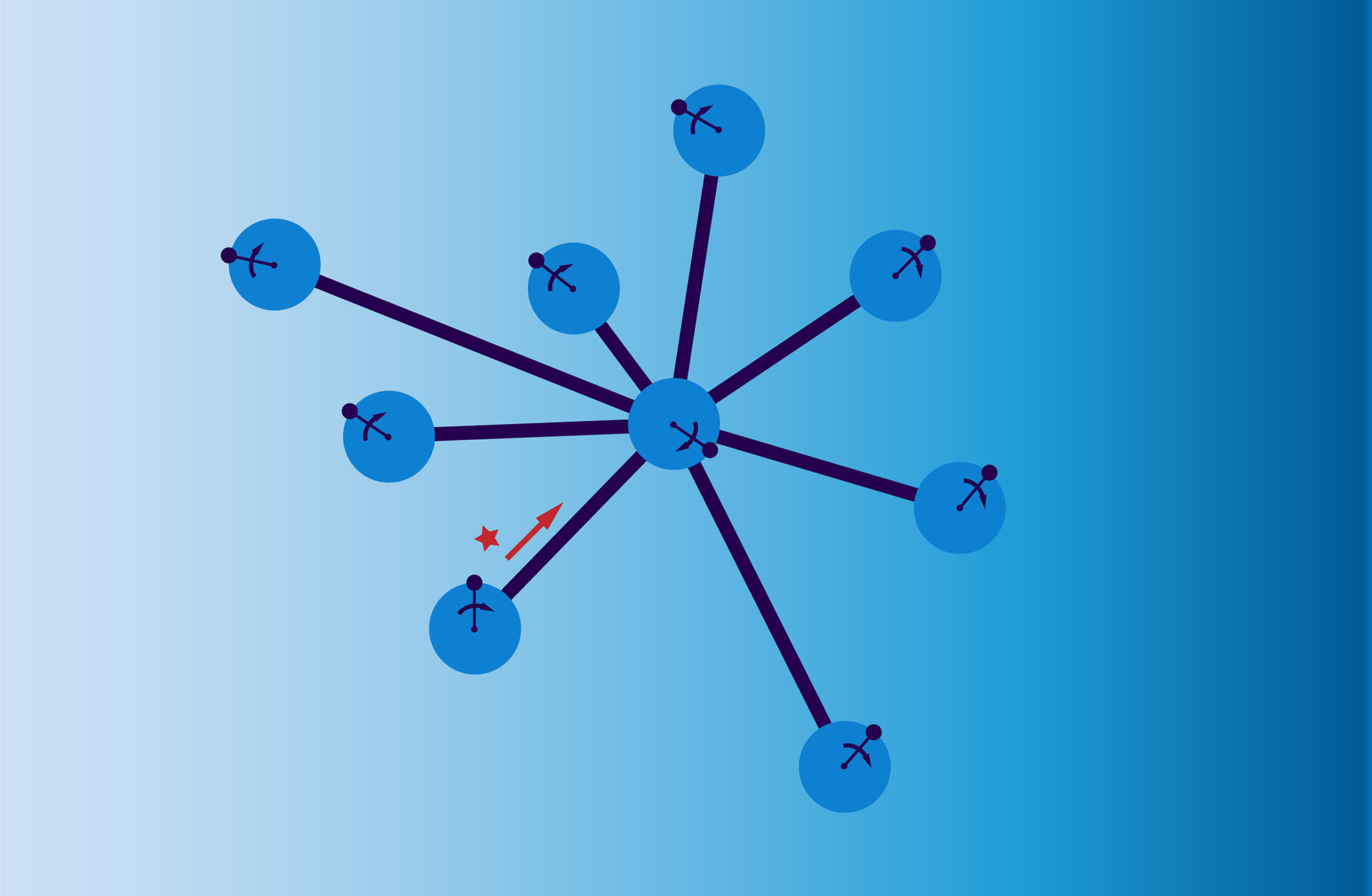
Certain oscillator networks suffer from deadlocks that prevent them from synchronizing. We derived the likelihood for such constellations in star graphs and found that they also occur in random graphs.
Written and illustrated by Christian Bettstetter
People dancing in groups, fish swimming in schools, and neurons firing in unison: the world is full of phenomena in which entities synchronize their behavior. They can be modeled as networks of coupled oscillators, where each entity has its own rhythm and interacts with other entities to promote the emergence of a common rhythm. Such convergence to synchrony has been investigated by scientists in many cases for different interaction strategies and various types of networks.
Synchronization is also a core topic of my research group at the University of Klagenfurt. We employ discrete coupling, where pulses or messages are exchanged at discrete points in time, to synchronize networked systems in a distributed way. On the applied side, we adapted the theory for wireless networks, proposed a technique to improve the synchronization precision, and experimentally assessed the system on programmable radios. On the theoretical side, we proposed the concept of stochastic coupling and performed convergence proofs in collaboration with Marc Timme and his team.
Our latest research centers on pulse-coupled oscillator networks that are sometimes unable to synchronize due to deadlocks. Doctoral student Arke Vogell explains: “If the system is in a deadlock, at least one entity is permanently prevented from firing and thus never synchronizes with the rest of the network.” The probability for such a situation to occur has been derived for the star graph as a special type of graph in which one hub is connected to multiple leaves. Star graphs play a prominent role in many systems and constitute basic subgraphs in complex networks, such as power grids and telecommunication systems. Simulations accompanying our mathematical analysis show that deadlocks are not restricted to star graphs but also occur in random graphs. In both graph types, it seems that deadlocks are more likely if the reaction of an entity to incoming pulses is strong, and they generally occur only at entities that have a certain minimum number of neighbors. Being aware of the deadlock phenomenon and its characteristics could support the design of network synchronization techniques.
Publication
Arke Vogell, Udo Schilcher, and Christian Bettstetter. Deadlocks in the Synchronization of Pulse-Coupled Oscillators on Star Graphs. Physical Review E, vol. 102, no. 6, article 062211, December 2020. Open access.
Press coverage
Alois Pumhösel. Self-Organization Along the Lines of Nature. Der Standard, January 2021.
This work was partly funded by the Austrian Science Fund (FWF), grant “Self-organizing synchronization with stochastic coupling” (P30012).